数据结构学习，其四，优先队列和堆

什么是优先队列

普通队列：先进先出，后进后出
优先队列：出队顺序和进队顺序无关，和优先级有关

实现的接口

与普通队列相同

用什么实现，时间复杂度分析

什么是堆（heap）

堆是二叉树的一种，堆是一课完全二叉树。完全二叉树不一定是满的二叉树，但在完全二叉树中，如果有缺，那么缺的一定是右下角的叶子节点。堆中某个节点的值总是不大于其父亲节点的值（此为最大堆）。

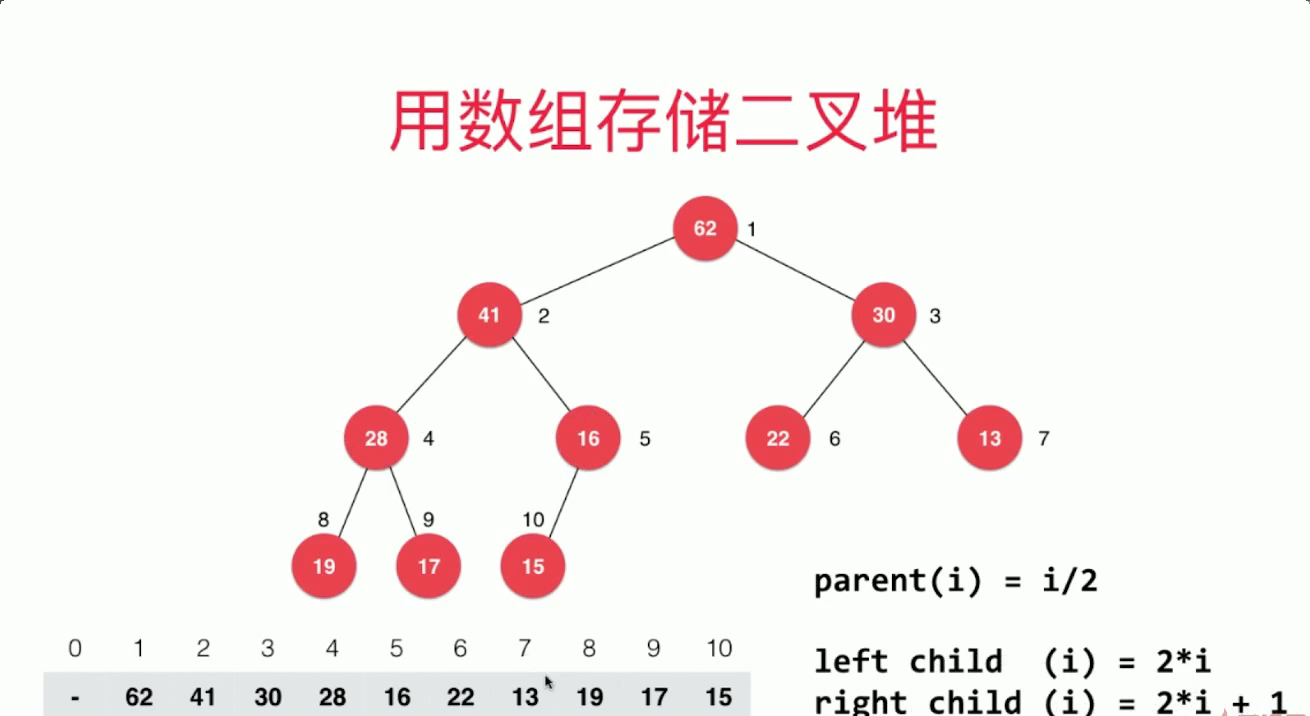
代码实现

public class MaxHeap<E extends Comparable<E>> {

    private Array<E> data;

    public MaxHeap(int capacity){
        data=new Array<E>(capacity);
    }

    public MaxHeap(){
        data=new Array<E>();
    }

      public MaxHeap(E[] arr){
        data=new Array<E>(arr);
        for (int i=parent(data.getSize()-1);i>=0;i--)
            siftDown(i);
    }


    //返回堆中的元素个数
    public int size(){
        return data.getSize();
    }

    //返回一个布尔值，表示堆中是否为空
    public boolean isEmpty(){
        return  data.isEmpty();
    }

    //返回完全二叉树的数组表示中，一个索引锁所表示的父亲节点的索引
    private int parent(int index){
        if (index==0){
            throw new IllegalArgumentException("index-0 doesn't hava parent.");
        }
        return (index-1)/2;
    }

    //返回完全二叉树的数组表示中，一个索引所表示的元素的左孩子节点的索引
    private int leftChild(int index){
        return index*2+1;
    }

    //返回完全二叉树的数组表示中，一个索引所表示的元素的右孩子节点的索引
    private int rightChild(int index){
        return index*2+2;
    }

    //向堆中添加元素
    public void add(E e){
        data.addLast(e);
        siftUp(data.getSize()-1);
    }

    private void siftUp(int k) {
        while (k > 0 && data.get(parent(k)).compareTo(data.get(k)) < 0) {
            data.swap(k, parent(k));
            k = parent(k);
        }
    }

    //看堆中最大元素
    public E findMax(){
        if (data.getSize()==0)
            throw new IllegalArgumentException("can't find max when heap is empty");
        return data.get(0);
    }


    //取出堆中最大元素
    public E extractMax(){
        E ret=findMax();

        data.swap(0,data.getSize()-1);
        data.removeLast();
        siftDown(0);

        return ret;

    }

    private void siftDown(int k) {
        while (leftChild(k)<data.getSize()){

            //找到左右节点中较大的那个节点的索引
            int j=leftChild(k);
            if (j+1<data.getSize() && data.get(j).compareTo(data.get(j+1))<0)
                j=rightChild(k);

            //data[j]是leftChild和rightChild的最大值
            if (data.get(k).compareTo(data.get(j))>=0)
                break;

            data.swap(k,j);
            k=j;
        }
    }

    //取出堆中的最大元素，并且替换成元素e
    public E replace(E e){
        E ret=findMax();
        data.set(0,e);
        siftDown(0);
        return ret;
    }

}