什么是集合?
和数学上的定义类似,集合就是“一堆东西”,比较关键的一点是,集合里的东西只能存在一次。非常适合用二分搜索树来实现。
用什么实现
根据集合的特性,我们可以使用链表或者二分树来实现。先来分析一下使用这2种结构实现的时间复杂度分析。

代码实现
//使用树实现
import BST.BST;
public class BSTSet <E extends Comparable<E>> implements Set<E>{
private BST<E> bst;
public BSTSet(){
bst=new BST<E>();
}
@Override
public void add(E e){
bst.add(e);
}
@Override
public int getSize(){
return bst.getSize();
}
@Override
public boolean isEmpty(){
return bst.isEmpty();
}
@Override
public boolean contains(E e){
return bst.contains(e);
}
@Override
public void remove(E e){
bst.remove(e);
}
}
//使用链表实现
import Stack.LinkedList;
public class LinkedListSet<E> implements Set<E> {
private LinkedList<E> list;
public LinkedListSet(){
list=new LinkedList<E>();
}
@Override
public void add(E e){
if (!list.contains(e)){
list.addFirst(e);
}
}
@Override
public int getSize(){
return list.getSize();
}
@Override
public boolean isEmpty(){
return list.isEmpty();
}
@Override
public boolean contains(E e){
return list.contains(e);
}
@Override
public void remove(E e){
list.removeElement(e);
}
}
什么是映射
在数学里,映射是个术语,指两个元素的集之间元素相互“对应”的关系,为名词。映射通常是key=>value形式的数据结构,根据键(key)来寻找值(value),非常容易使用链表或者二分搜索树实现。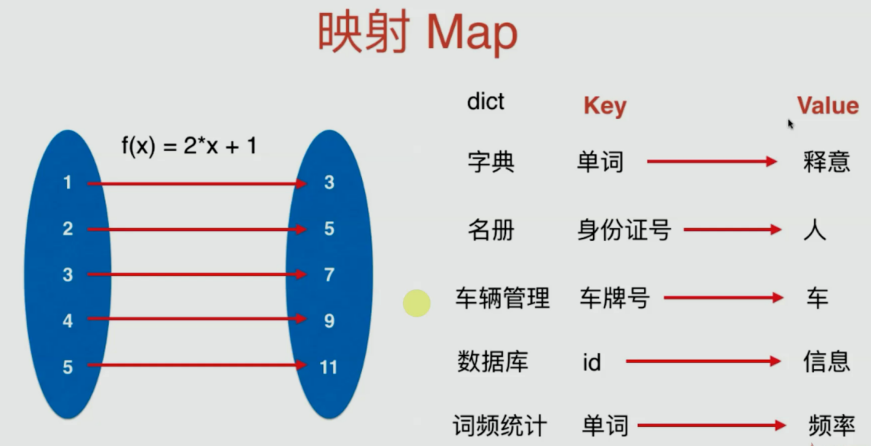

映射需要实现的接口
public interface Map<K,V> {
void add(K key, V val);
V remove(K key);
boolean contains(K key);
V get(K key);
void set(K key,V val);
int getSize();
boolean isEmpty();
}
代码实现
//树实现
public class BTSMap<K extends Comparable<K>,V> implements Map<K,V> {
private class Node {
public K key;
public V val;
public Node left, right;
public Node(K key,V val) {
this.key = key;
this.val = val;
left = null;
right = null;
}
}
private Node root;
private int size;
public void BSTMap(){
root=null;
size=0;
}
@Override
public int getSize(){
return size;
}
@Override
public boolean isEmpty(){
return size==0;
}
@Override
public void add(K key,V val){
root = add(root, key, val);
}
private Node add(Node node, K key,V val){
if(node == null){
size ++;
return new Node(key,val);
}
if(key.compareTo(node.key) < 0)
node.left = add(node.left, key,val);
else if(key.compareTo(node.key) > 0)
node.right = add(node.right, key,val);
else //key.compareTp(node.key)==0
node.val=val;
return node;
}
//返回以node为根节点的二分搜索树中,key所在的节点
private Node getNode(Node node,K key){
if (node==null)
return null;
if (key.compareTo(node.key)==0)
return node;
else if (key.compareTo(node.key)<0)
return getNode(node.left,key);
else //key.compareTp(node.key)>0
return getNode(node.right,key);
}
@Override
public boolean contains(K key){
return getNode(root,key)!=null;
}
@Override
public V get(K key){
Node node=getNode(root,key);
return node==null?null:node.val;
}
@Override
public void set(K key,V val){
Node node=getNode(root,key);
if (node==null)
throw new IllegalArgumentException(key+"doesn't exist!");
node.val=val;
}
//返回以node为根的二分搜索树的最小值所在的节点
private Node minimun(Node node){
if (node.left==null)
return node;
return minimun(node.left);
}
//从二分搜索树中删除最小值所在的节点,返回根节点
private Node removeMin(Node node){
if (node.left==null){
Node rightNode=node.right;
node.right=null;
size--;
return rightNode;
}
node.left=removeMin(node.left);
return node;
}
//从集合中删除为key的节点
@Override
public V remove(K key){
Node node=getNode(root,key);
if (node!=null){
remove(root,key);
return node.val;
}
return null;
}
//删除掉以node为根的二分搜索树中键为key的节点,递归算法
//返回删除节点后新的二分搜索树的根
private Node remove(Node node, K key) {
if (node==null)
return null;
if (key.compareTo(node.key)<0){
node.left=remove(node.left,key);
return node;
}
else if (key.compareTo(node.key)>0){
node.right=remove(node.right,key);
return node;
}else {//key.compareTo(node.key)==0
if (node.left==null){
Node rightNode=node.right;
node.right=null;
size--;
return rightNode;
}
if (node.right==null){
Node leftNode=node.left;
node.left=null;
size--;
return leftNode;
}
Node newNode=minimun(node.right);
newNode.left=node.left;
newNode.right=removeMin(node.right);
node.left=node.right=null;
return newNode;
}
}
public static void main(String[] args) {
BTSMap<Integer,Integer> bstmap=new BTSMap<Integer,Integer>();
bstmap.add(3,3);
bstmap.add(2,2);
bstmap.add(1,1);
System.out.println(bstmap.size);
System.out.println(bstmap.get(2));
bstmap.remove(2);
System.out.println(bstmap.get(2));
}
}
//链表实现
public class LickedListMap<K,V> implements Map<K,V> {
private class Node{
public K key;
public V val;
public Node next;
public Node(K key,V val,Node next){
this.key=key;
this.val=val;
this.next=next;
}
public Node(K key){
this(key,null,null);
}
public Node(){
this(null,null,null);
}
@Override
public String toString(){
return key.toString()+":"+val.toString();
}
}
private Node dummyHead;
private int size;
public LickedListMap(){
dummyHead=new Node();
size=0;
}
@Override
public int getSize(){
return size;
}
@Override
public boolean isEmpty(){
return size==0;
}
private Node getNode(K key){
Node cur=dummyHead.next;
while (cur!=null){
if (cur.equals(key)){
return cur;
}
cur=cur.next;
}
return null;
}
@Override
public boolean contains(K key){
return getNode(key)!=null;
}
@Override
public V get(K key){
Node node=getNode(key);
return node==null?null:node.val;
}
@Override
public void add(K key,V val){
Node node=getNode(key);
if (node==null){
dummyHead.next=new Node(key,val,dummyHead.next);
size++;
}else {
node.val=val;
}
}
@Override
public void set(K key,V newVal){
Node node=getNode(key);
if (node==null){
throw new IllegalArgumentException(key+"doesn't exist!");
}
node.val=newVal;
}
@Override
public V remove(K key){
Node prev=dummyHead;
while (prev.next!=null){
if (prev.next.val.equals(key)){
break;
}
prev=prev.next;
}
if (prev.next!=null){
Node delNode=prev.next;
prev.next=delNode.next;
delNode.next=null;
size--;
return delNode.val;
}
return null;
}
}